Jak badać rozkład dwóch zmiennych?
Jak badać łączny rozkład dwóch zmiennych ilościowych?
Do analizy zależności dwóch zmiennych ilościowych najczęściej stosuje się współczynniki korelacji liniowej (Pearsona) i monotonicznej (Spearmana).
Jednak zawsze o ile czas i miejsce na to pozwala należy uzupełnić taką analizę analizą graficzną (kiedy może nie pozwalać? Jeżeli badać chcemy korelacje dla 1000 zmiennych, każdej z każdą nie narysujemy).
Pokażmy przykłady kiedy i jak poradzą sobie te współczynniki. Wykorzystamy do tego kwartet Francisa Anscombe'a.
library(ggplot2)
attach(anscombe)
cor(x1, y1)
## [1] 0.8164205
cor(x1, y1, method="spearman")
## [1] 0.8181818
ggplot(anscombe, aes(x1, y1)) + geom_point() + geom_smooth(method="lm", color="grey", se=FALSE)
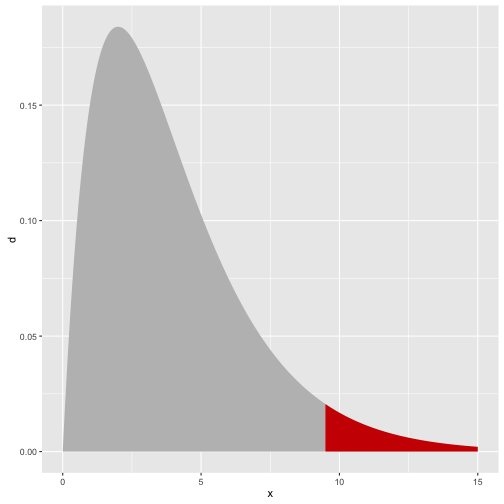
cor(x2, y2)
## [1] 0.8162365
cor(x2, y2, method="spearman")
## [1] 0.6909091
ggplot(anscombe, aes(x2, y2)) + geom_point() + geom_smooth(method="lm", color="grey", se=FALSE)
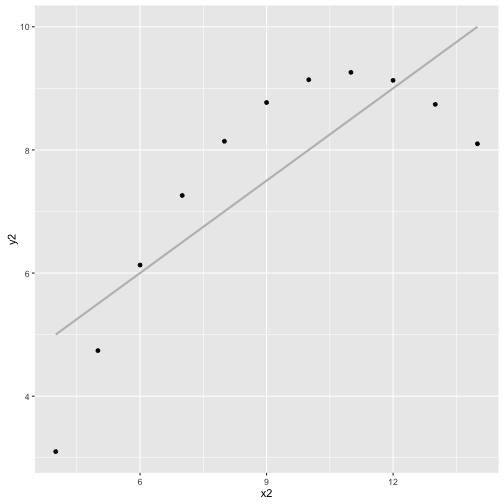
cor(x3, y3)
## [1] 0.8162867
cor(x3, y3, method="spearman")
## [1] 0.9909091
ggplot(anscombe, aes(x3, y3)) + geom_point() + geom_smooth(method="lm", color="grey", se=FALSE)
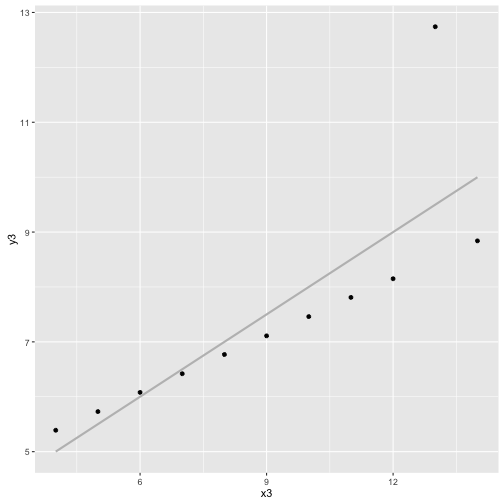
cor(x4, y4)
## [1] 0.8165214
cor(x4, y4, method="spearman")
## [1] 0.5
ggplot(anscombe, aes(x4, y4)) + geom_point() + geom_smooth(method="lm", color="grey", se=FALSE)
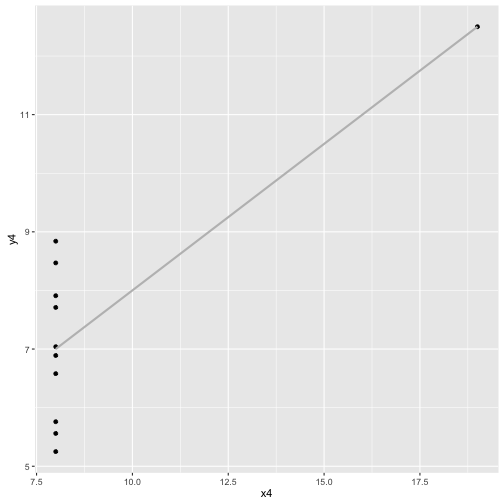
Jak badać łączny rozkład dwóch zmiennych jakościowych?
Łączny rozkład pary zmiennych jest często przedstawiony za pomocą tablicy kontyngencji, macierzy liczb.
Jednak nawet małe macierze jest często trudno zrozumieć. Analiza korespondencji jest techniką, która może to umożliwić / ułatwić.
Tabela kontyngencji
Rozważmy macierz zliczeń dla pary zmiennych, oznaczmy ją przez
| Y \ X | ||||
|---|---|---|---|---|
| ... | ||||
| ... | ... | ... | ||
| ... |
Aby zbadać współwystępowanie poziomów, wygodniej jest pracować na macierzy znormalizowanej, oznaczmy ją przez
gdzie oznacza kolumnowy wektor jedynek o długości .
W kolejnym kroku wyznaczmy brzegowe częstości, oznaczmy je jako wektory
Możemy teraz wyznaczyć różnicę pomiędzy obserwowaną macierzą częstości a oczekiwaną, przy założeniu niezależności.
Dekompozycja
Z macierzy można odczytać, które komórki występują częściej niż wynikałoby to z przypadku. Jednak wciąż tych liczb jest tak dużo, że trudno je wszystkie zauważyć.
W celu prezentacji całej macierzy stosuje się uogólnioną dekompozycję SVD na trzy macierze
takie, że i są ortonormalne względem wektorów i a jest macierzą diagonalną. Czyli
Czasem wyprowadza się ten rozkład jako zwykłe SVD ze znormalizowanej macierzy .
Diagonalna macierz określa wkład kolejnych wektorów w wyjaśnienie macierzy .
Jeżeli elementy w odpowiadających sobie kolumnach macierzy i mają ten sam znak, to przełożą się one na wartość dodatnią w odpowiadającej im komórce macierzy .
Na wykresie zazwyczaj przedstawia się ładunki odpowiadające dwóm największym wartościom z macierzy . Im bliżej siebie i dalej od początku układu współrzędnych są poszczególne wartości, tym częstsze ich współwystępowanie.
Przykład
Przeprowadźmy graficzną analizę korespondencji dla danych o kolorach oczu i włosów.
library(ca)
(tab <- HairEyeColor[,,1])
## Eye
## Hair Brown Blue Hazel Green
## Black 32 11 10 3
## Brown 53 50 25 15
## Red 10 10 7 7
## Blond 3 30 5 8
anacor <- ca(tab)
plot(anacor)
summary(anacor)
##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.134288 90.8 90.8 ***********************
## 2 0.013275 9.0 99.7 **
## 3 0.000395 0.3 100.0
## -------- -----
## Total: 0.147958 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | Blck | 201 997 339 | -495 979 366 | 67 18 67 |
## 2 | Brwn | 513 890 11 | -50 767 10 | 20 123 15 |
## 3 | Red | 122 999 78 | 62 40 3 | -302 958 838 |
## 4 | Blnd | 165 999 572 | 711 987 621 | 80 13 80 |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | Brwn | 351 999 458 | -438 993 501 | 36 7 35 |
## 2 | Blue | 362 1000 374 | 379 940 387 | 96 60 250 |
## 3 | Hazl | 168 943 32 | -128 579 21 | -101 364 130 |
## 4 | Gren | 118 996 136 | 322 610 91 | -256 386 585 |
Zadania
Symulacyjnie zbadaj moce testów Spearmana i Pearsona jako funkcje wielkości próby. Porównaj wyniki dla różnych rozkładów korelowanych zmiennych.